[원자력기사 기출풀이] 2021년 2차 원자력기초 11 ~ 15번

 

 

 

11. 핵분열에 대한 설명 중 틀린 것은?
    ① Th-233은 중성자를 흡수한 후 핵분열성물질로 전환된다.
    ② U-233은 핵분열 당 생성되는 평균 중성자는 2 ~ 3개이다.
    ③ U-238의 핵분열 시 생성되는 에너지는 약 200 MeV이다.
    ④ U-235의 핵분열 시 생성되는 에너지의 대부분은 중성자의 에너지이다.

 

1. Th-232는 중성자를 흡수하여 U-233으로 전환되는 Fertile 핵종이다.

아마 복원이 잘못된 듯 하다....

 

2. 분열시 방출하는 중성자의 갯수를 $\nu$ 값이라고 하는데, 핵종마다 다르지만 2 ~ 3 사이에 있다.

 

3. U-238은 속중성자와 반응하여 속핵분열을하고 U-235와 비슷하게 200 MeV 정도의 에너지를 방출한다.

 

4. 분열시 방출되는 에너지 ( Q값) 의 대부분. 170 MeV 정도는 두 핵분열생성물의 운동에너지 형태로 전달된다.

 

나머지는 

즉발감마 7 MeV

즉발중성자 5 MeV

 

지발감마 : 6 MeV

베타붕괴 : 6.5 MeV

중성미자 : 9 MeV

정도의 형태로 방출된다.

 

 

 

정답 : 1, 4번

---

12. 원자로 내의 한 지점에서 중성자의 수밀도가 $1.0×10^9 /cm^3$이고, 이 지점에서 핵분열 반응 수가 $2.2×10^{13} /cm^3 · sec일 때, 핵연료의 거시적 핵분열 단면적은 얼마인가?
(단, 중성자 속력은 2,200 m/sec이다.)
    ① 0.1 /cm     ② 0.2 /cm     ③ 0.3 /cm    ④ 0.4 /cm

 

반응률 RR :  Reaction Rate 단위체적당 단위시간당 반응 수, [  $ / cm^3 / sec ]

$$ RR = 2.2*10^{13} = \Sigma\phi = \Sigma nv = \Sigma * 1*10^9 * 220000 cm/sec $$

 

따라서 거시적단면적은 0.1 /cm

 

정답 : 1번

---

13. 다음 중 핵반응단면적에 대한 설명 중 틀린 것은?
    ① 1barn은 $10^{-24} cm^2$이다.
    ② 거시적단면적은 미시적단면적에 단위체적 당 원자핵의 수를 곱한 값이다.
    ③ U-235의 핵분열단면적은 중성자 에너지가 특정 값 이상일 때, 0이다.
    ④ U-238은 특정 중성자에너지 영역에서 흡수단면적이 매우 커지는 공명흡수영역을 갖는다.

 

1 barn : 미시적 단면적($\sigma$)의 단위. $1 barn = 1*10^{-24} cm^2$

 

거시적 단면적 $\Sigma$ : 단위거리진행당 반응확률로서, 미시적단면적과 원자밀도를 곱한 값임. 즉,

$$\Sigma = N * \sigma = \frac{\rho N_A}{A} * \sigma$$

$N_A$ 는 아보가드로 수.

 

U-235은 fissle 핵종으로서, 어떤 에너지의 중성자를 흡수하더라도 핵분열이 가능한 핵종이다.

 

위 표를보면 U-235가 분열하기 위해서는 6.5 MeV의 에너지가 더 필요하다. 중성자가 U-235와 결합하여 복합핵 U-236을 형성할 때, 6.8 MeV의 에너지를 방출하므로, 아주 약한 에너지의 중성자가 반응하더라도 핵분열이 가능하다.

맨 오른쪽 열의 Be - E_crit이 양수면 문턱에너지가 없는 것이고, Th-232나 U-238 같이 음수이면 그만큼의 에너지를 가진 중성자가 필요하다.

 

 

 

공명흡수영역 : 열외중성자 구간에서 흡수단면적이 빠르게 진동하듯이 변하는 구간.

 

위 그림은 핵물질들의 공명흡수영역을 보여준다.

U-238 뿐만아니라 다른 핵물질들도 공명흡수 영역이 있다.

 

 

정답 : 3번

---

14. 2 MeV의 속중성자가 중수소와 충돌하여 1 eV의 열중성자로 감속될 때까지 평균 충돌 횟수는?
    ① 10     ② 20     ③ 30    ④ 40

 

중성자의 충돌후 평균 에너지는 다음과 같다.

$$E_1 = E_0 * \frac{1+\alpha}{2} = 0.556E_0$$

 

여기서 

$\alpha = (\frac{M-m}{M+m})^2 = 0.111$

 

이고,

M : 매질의 질량수, 중수소의 경우 2

m : 중성자의 질량수 1

E1 : 충돌 후 에너지

E0 : 충돌 전 에너지

이다.

 

N 번 충돌 후에는,

$E_n = 0.556^nE_0$ 에서

$E_n = 1 eV$

$E_0 = 2 MeV $

를 대입하면

 

n = 24.7.

 

평균 24.7 회 충돌함.. 답이 애매하다. 

중수소가 아니라 수소면, $\alpha = 0$ 이되고 n = 20.9 가 된다.

복원이 잘못된 듯 하다.

 

정답 : ??

---

15. 반사체가 없는 직육면체 균질로에서 노심출력의 평균값에 대한 최대값의 비율(Average to Max Ratio)은? (단, 직육면체 경계면에서 중성자속은 0으로 가정한다.)
    ① $π/2$       ② $π^2 /3$       ③ $π^3 /8$     ④ $π^4 /16$

 

 

Introduction to Nuclear Engineering. John. R. Lamarsh

 

노심 출력의 평균값에 대한 최대값 비율은 위 표에서 $\Omega$ 이다.

 

출력은 중성자속 Flux에 직접적으로 비례한다. 

 

직육면체의 중성자속은 표에서 확인할 수 있다.

 

최대값은 당연히 노심 중앙일 것이고, x = y = z = 0에서 최대값일 것이다. 

이 때 값은 A 이다.

 

평균중성자속은 중성자속을 전체 부피에 대해 적분한 다음에 부피로 나눠주면 되는데,

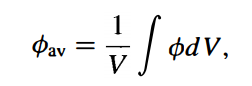
직교좌표계에서 간단하게 계산되며

$\phi_{avg} = (2/\pi)^{3} A$

 

이다.

 

따라서

$\phi_{max} / \phi_{avg} = {\pi}^3/8 $

 

이다.

 

 

 

정답 : 3